Работа ученых Санкт-Петербургского политехнического университета Петра Великого украсила обложку ведущего научного журнала Лондонского королевского общества – Proceedings of the Royal Society A. В своей статье петербургские ученые предложили оригинальную теорию описания структуры икосаэдрических квазикристаллов, приблизив тем самым ученых всего мира к решению одной из важнейших задач современного материаловедения.
Авторитет журналов Королевского общества сложно переоценить. Ведь на их страницах впервые были опубликованы закон Джоуля, теория эволюции Дарвина, уравнения Максвелла и опыты Резерфорда. Здесь впервые появились описание двойной спирали ДНК, предложенное Д. Уотсоном и Ф. Криком, расшифровка структуры гемоглобина М. Перутцем, и другие выдающиеся работы. По публикациям этого журнала можно изучать историю развития современной физики, начиная ещё со времён Ньютона. И тот факт, что работа петербургского учёного украсила обложку, говорит о высоком уровне результата и мировом признании.
Алексей Евгеньевич Мадисон, ведущий научный сотрудник Центра перспективных исследований СПбПУ, на протяжении нескольких лет занимается теорией квазикристаллического состояния. И главная задача, стоящая перед ним – это описание и расшифровка структуры икосаэдрических квазикристаллов.
До недавнего времени строение квазикристаллов рассматривалось в рамках шестимерной кристаллографии, что сильно усложняло расчеты и не позволяло получить простую и наглядную картину. Однако, в 2015-м году, благодаря работам ученого из Политехнического университета появилась возможность решения данной проблемы в трехмерном пространстве.
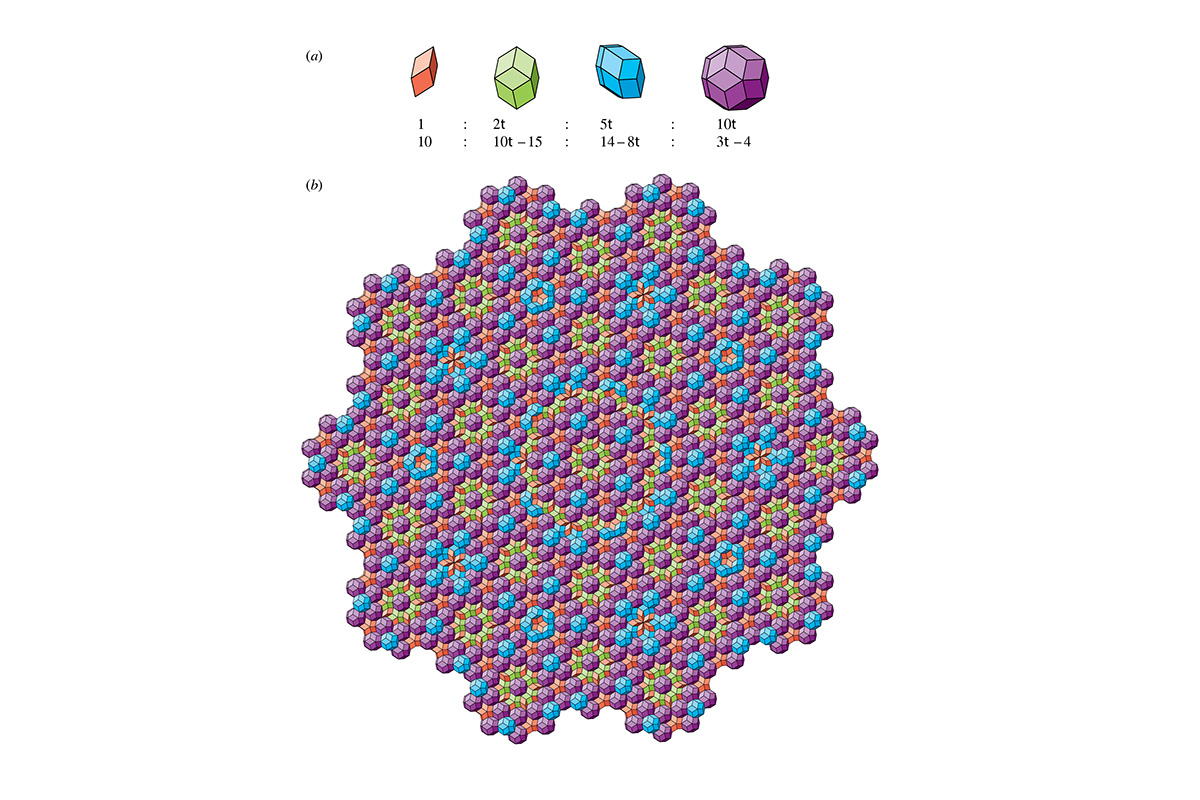
«Всё, как в обычных кристаллах, с единственными отличиями – имеется четыре типа элементарных ячеек вместо одной, а заполнение пространства идентичными копиями ячеек идёт по принципу самоподобия, а не трансляции», – поясняет Алексей Евгеньевич.
Расположение атомов в структуре кристалла определяется на основе анализа дифракционных картин. Уравнение дифракции для обычных кристаллов предложил Уильям Брэгг, став самым молодым Нобелевским лауреатом в истории. Сейчас каждый студент знает, что если в кристалле на разности хода между двумя последовательными атомными плоскостями укладывается целое число длин волн, то рассеянные лучи придут в одной фазе, давая при определённых углах резкие дифракционные пики.
А что если расстояния между соседними плоскостями не равны друг другу, а чередуются, например, в соответствии с последовательностью Фибоначчи? Будут ли появляться Брэгговские пики, или будет присутствовать только лишь диффузный фон? На этот вопрос в 1982 году ответил Дан Шехтман, поразив научное сообщество дифракционной картиной с симметрией пятого порядка. Это противоречило основному закону кристаллографии, согласно которому оси 5-го порядка несовместимы с периодической решёткой. После долгой борьбы с неприятием нового, в 2011-м году Дан Шехтман был удостоен Нобелевской премии.
В квазикристаллах любой фрагмент структуры повторяется бесконечно много раз, повторяется строго закономерно, но отнюдь не периодически. Определить разность хода между выбранной плоскостью и каждой последующей, а затем ещё и усреднить соответствующие фазовые множители казалось просто невозможным. Однако Алексей Евгеньевич нашел неожиданное решение – он предложил построить специальную матрицу по аналогии с матрицей подстановок, только её элементами должны быть комплексные фазовые множители. Далее остаётся провести анализ этой матрицы на собственные значения и собственные числа в рамках теории Перрона-Фробениуса. В итоге задача сводится к вычислению парциальных структурных факторов для каждого типа квазиэлементарных ячеек, а проецирование Перрона дает искомые комплексные весовые коэффициенты для их усреднения по всему объёму.
Благодаря полученным результатам, ученые ещё на один шаг приблизились к расшифровке структуры квазикристаллов. И очень символичным кажется тот факт, что решение задачи о дифракции на квазикристаллах (не использующее концепции шестимерных гиператомов) появилось на страницах того же журнала, где более 100 лет назад было опубликовано уравнение Вульфа-Брэгга.
Материал подготовлен Сектором научных коммуникаций. Текст: Мария ГАЙВОРОНСКАЯ
